摘要🔖：

統計分析對於進行（數字化）體能訓練的起著至關重要的作用🚣🏿，不論數據之間的差異和相關性是什麽🍜，教練都應該能夠識別其信度與客觀性。這些分析技能是我們能去發現某些數據所呈現的趨勢和它們之間的內在聯系，可為將來的訓練計劃作出有效預判性設計和評估。本文通過Microsoft Excel進行了測試統計👰‍♀️🧼，包括了信度（通過變異系數），最小的有價值的變化量（例如，數值中第一個有意義的差異）⛏，效應量（ES,運動表現相關測試中的的明顯數值變化）💁🏻，以及關聯關系（即相關性）。

關鍵詞：最小有價值的變化；效應量；相關性；變異系數

一🚵🏼、前言

數據分析涉及統計，或者說涵蓋了數據收集✍🏽🦷、分析和客觀解釋的科學（包括推論）🫃🏼🤸🏿‍♂️。統計的關鍵是客觀性，使它產生的結果可以不受偏見和個人動機的影響。使用統計數據可以讓我們發現趨勢和其關聯🦸🏻、做出預測以及評估針對體能測試流程和運動員身體特征的訓練計劃的有效性👎🏿🦴。因此🧛‍♀️，統計數據對於體能教練而言至關重要，從業人員應該熟悉分析數據的不同方法且隨後與教練和運動員對這些數據進行溝通。

我們旨在介紹幾種可以進行與體能相關的統計分析的方法。選擇的測試是可以使用Microsoft Excel（Excel，Microsoft，Redmond👇🏽，Washington）進行，因此這也適用於大多數讀者。具體來說，我們將研究信度（通過變異系數[CV]）🤴🏼、最小的有意義的變化[SWC]（即數據的第一個有意義的差異），效應量（ESs🤷🏼‍♀️🦤，即效果之間的變化幅度）和數據之間關系（即相關性💁🏻，correlations）。盡管我們應該認識到這些分析方式也可以通過其他的方法，但是這些分析模式通常需要更專業的軟件🌟，如SPSS，IBM，Armonk，New York等這類社會科學統計軟件。在進行一系列的基礎體能測試之後🏔，我們將結果用本研究背景情況下的數據處理進應用進行討論💏。當然，我們也應該弄清楚如何將此過程推廣到其他方案。我們的分析從系統性偏差開始🧑🏼‍🦲。

關鍵詞：最小的有價值的變化；規模效應；相關性🪳；變異系數

二、系統性偏差

當我們試圖確定運動員的跳躍高度時，通常給運動員2次或3次重復測試以確定測試值的最大值。作為體能教練，我們會記錄所有測試，以便我們評估數據的信度（請參閱下文的信度部分）。在所有測試中我們可能會註意到🚆🌹，由於測試動作本身導致疲勞（不夠充分的休息間歇）的產生或者是動搖了測試動機👨🏻‍🏫，測試得到的結果會逐漸變差；當然也有可能由於不斷完善的動作技能（即學習效應）可能會導致測試結果越來越好。這種可能會發生的事被稱為系統性偏差，並且在做實驗設計環節時就應該盡可能規避🧑🏻‍🦱🫸🏿。

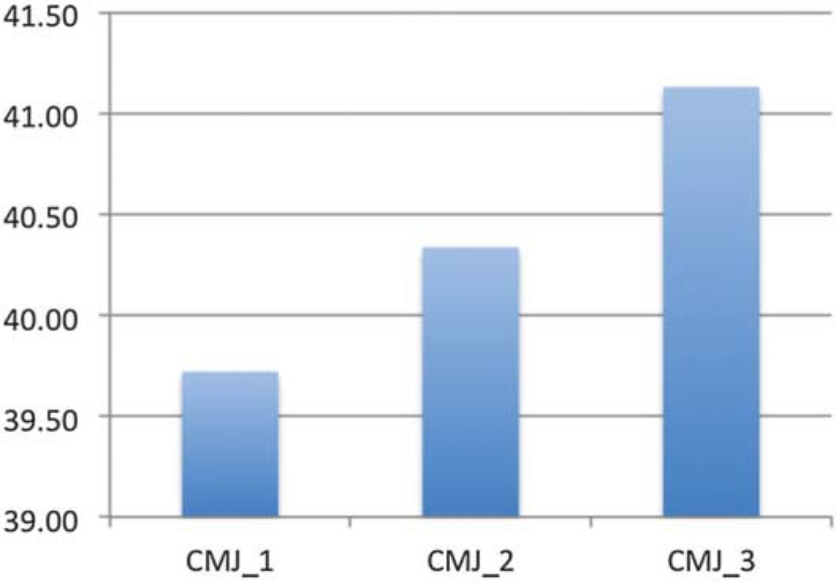
圖1 反向跳（CMJ）在3次測試中的變化🦸🏼。不難發現測試成績越來越好

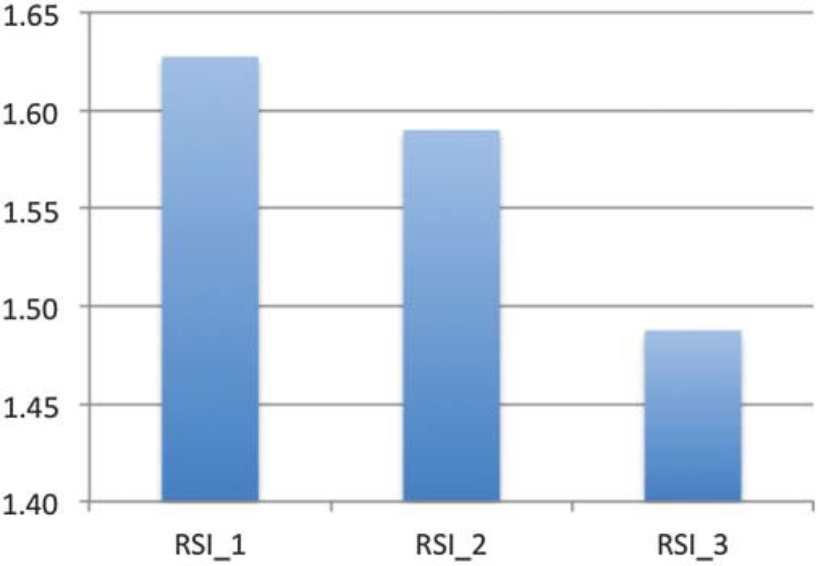
圖2 反應性力量（reactive strength）在三次測試中的變化。不難發現成績越來越差

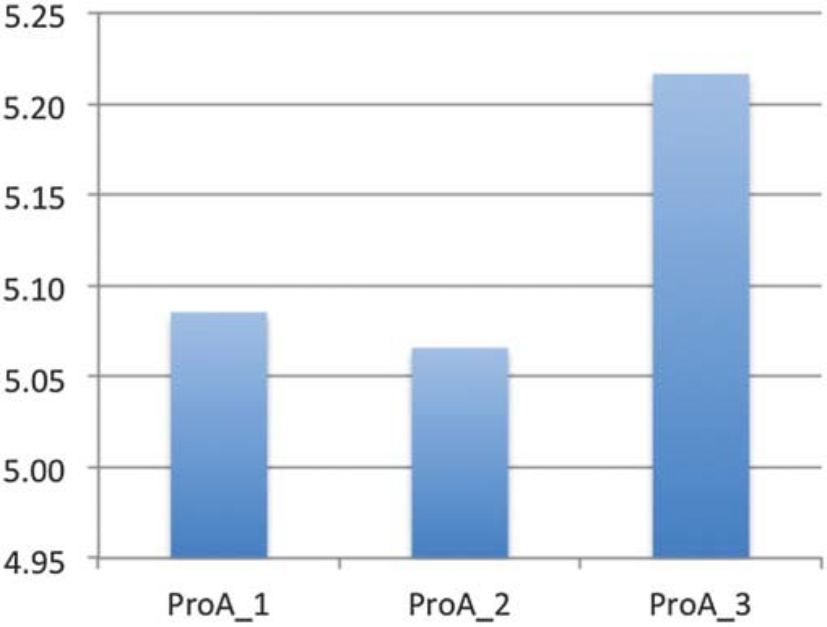
圖3 專業靈敏測試（Pro agility test🤵🏼‍♀️❗️，PorA）在三次測試成績的變化。不難發現第二次成績變好了，第三次變差了

圖4 在Excel中輸入數據時，要確保每行只添加1名運動員🏩。突出顯示標題單元格和意思單元格，並從“圖表”選項中選擇“列”。本圖中突出顯示的單元格（數字39.72）將生成圖1中所示的圖表🫄🏼。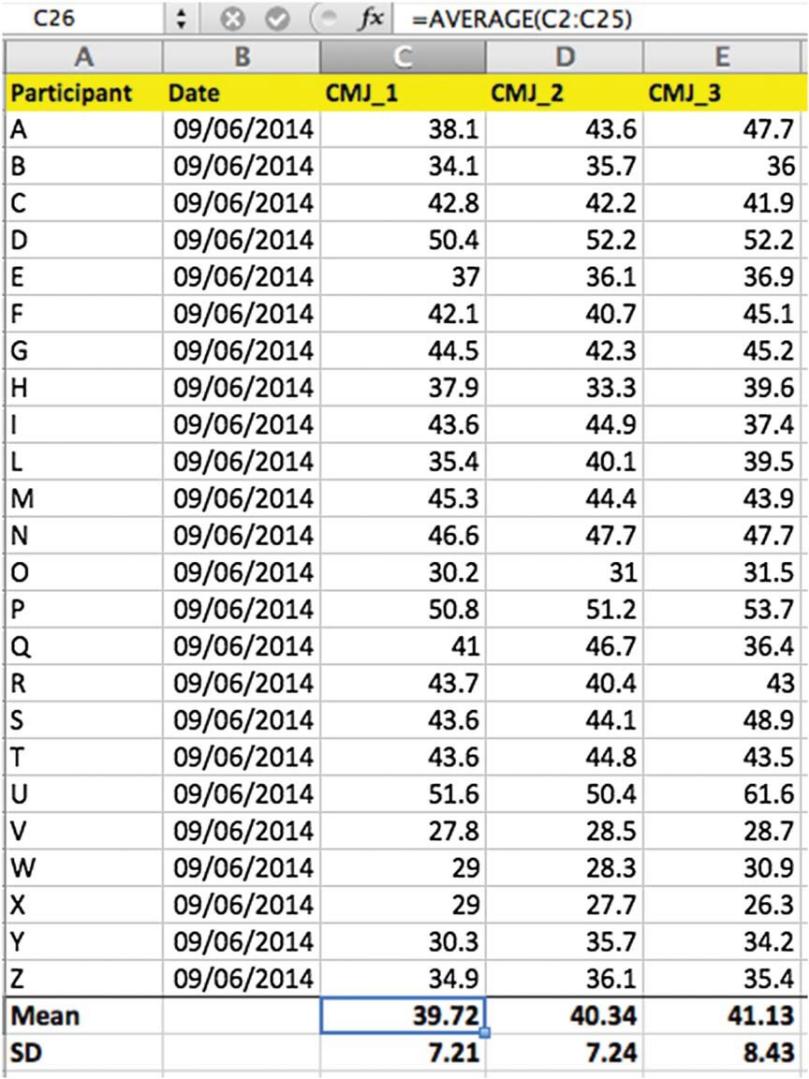

圖5 為了計算每個運動員的變異系數(CV)🔐，我們可以使用在公示欄中輸入公式🔗。它可以計算所有測試的標準差，然後計算平均值，再將他們乘以100%🚓，得到每個運動員的CV百分比。單擊該單元格的右下角(即正方形)將公式向下拖動並應用於所有運動員。

例如，在圖1中🧑🏽‍✈️，可以明顯看出運動員在反向跳(CMJ)高度上的數據隨著每次測試的進行而不斷提高🧑‍🤝‍🧑，從這個結果我們可以認為運動員由於每次動作技能的習得使得成績變得更好，或者有可能是運動員開始測試時“很冷”（沒激活該動作模式），測試人員可能沒有提供足夠的熱身或熟悉動作的時間。在這兩種情況下，獲得的數據可能都不可靠，可能需要至少包含1個其他測試才能確定運動員的真正最優運動表現。相反，在圖2中🐅，對於測試反應性力量（RSI）時，我們可以看到相反的結果🔅。在這種情況下👳‍♂️，也許是提供了太多的熱身，或者在兩次測試之間沒有給予足夠的休息，導致運動員感到疲勞。最後，在圖3中提供的專業靈敏測試時（Pro-Agility test，ProA）測試結果示例中，其實可能前兩個測試結果就夠了𓀊，因為第3個結果導致了運動表現的下降，這可能是由於疲勞或失去測試動機所致。因此，評估數據的一個很好的起點是檢查系統性偏差，即運動員準備測試的準備程度。

我們是可以使用Excel評估此過程（圖4）🧚🏽‍♂️。遵循以下準則以消除此類系統性誤差所導致的問題：

•確保運動員體溫已經升高（通過提高體溫，運動表現會有所改善）；

•提供一個熟悉期/熟悉課避免由於學習效果而測試結果不正常地迅速提高🛢；

•在兩次測試之間提供充足的休息時間確保疲勞不會對測試成績產生負面影響；

•測試工作人員應該保持始終如一的動機激勵-要麽全程鼓勵，要麽全程不說話。

三、信度

信度是指測試或測量的一致性或可靠性，或者說信度是可以作為所有測試的結果和發現的計算💒、認知的一種統計👌🏻。憑借信度，我們可以確保測試結果能夠提供準確的數據。例如🚱，如果你在3次完全一致的測試中得到運動員的30m沖刺時間🍶，每次的結果都明顯不同，則這種測試不能反映運動員的運動表現，這當然也就不可靠。當然，沒有測試是完全可以規避錯誤的——設備、測試操作員和運動員都會產生這些問題。

因此🤰🏽🧎🏻‍♂️‍➡️，我們必須決定可接受的誤差是多少✖️，並認識到運動員測試的成績真實值應該是在數據值±誤差的範圍內的。例如🩲，如果一名運動員在3秒鐘內跑了30 m，而測試中的誤差產生了0.5秒，則實際上該運動員是在2.5到3.5秒之間這個範圍跑了30 m。如果運動員在接下來的一個月重新測試，並且跑出2.6秒😰，他沖刺真的變得更快了嗎?

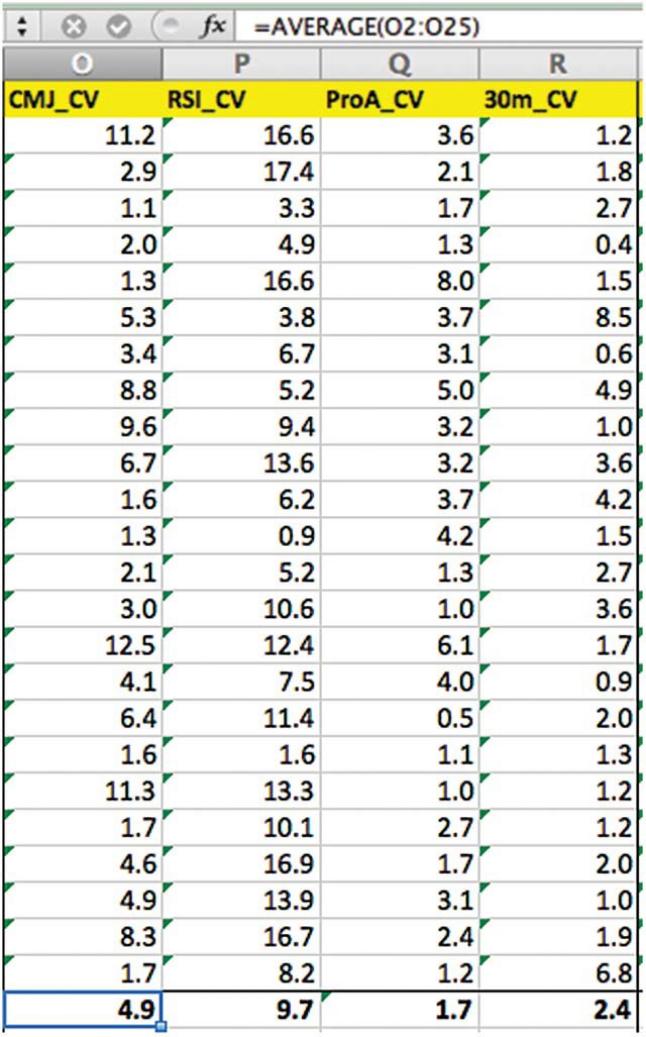
圖6 我們已經分別計算了每個運動員的變異系數（CV）🦠。接下來，我們使用公式欄中所示的“平均”公式對全隊的這些數據進行平均。對於CMJ來說🤚🏽6️⃣，CV= 4.9％表示可接受的信度。因此，如果運動員A跳了47.7厘米（圖4）🧗🏿‍♀️，則他的數據實際上在45.4到50厘米之間（47.7厘米*0.049=2.3厘米）。

我們將在此處使用的信度測試是變異系數（CV）🎀。CV是一種關於比率的統計，以一致性的百分比去提供數據信度。因為在體育運動中🥣，運動員通常只進行幾次測試(2-5次)，所以最好計算每個運動員的CV，然後計算整個團隊的平均值🤽🏽⏮。CV的計算如公式1和圖5💐、圖6所示。當測試目標的CV≤10%的時候就被科學界認為是具有信度的。不過對於體能測試來說，≤5%的CV值可能更加準確。還要註意的是，使用此方法可為每位運動員提供一個CV值，該值可用於控製運動員之間的一致性差異👨‍👩‍👦。然而通常情況下，團隊平均值的應用更為普遍。

CV =100（SD/M）. (公式1)

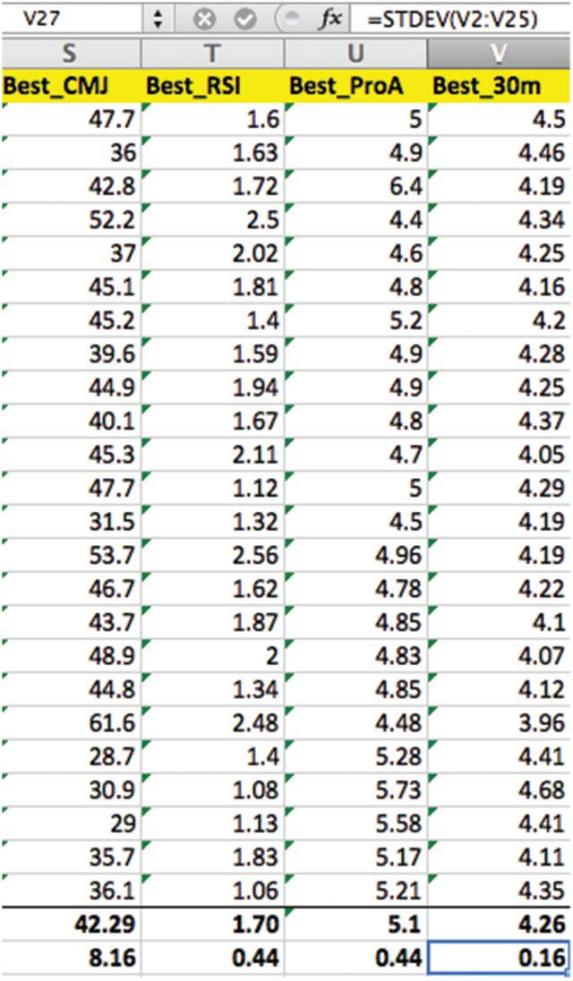
圖7 公式欄顯示了30m沖刺時間的標準差的計算，等於0.16s。

四👩🏿、最小的有價值的變化

假設數據是可靠的並且沒有系統性偏差，我們可以分析最小有價值的變化SWC（3），即可以接受真實數據的最小變化是多少？例如，如果一名運動員在季前測試期間能2.1秒內進行了30米的短跑測試，然後在進行訓練幹預後數據為2.0s，則可能會認為由於某些其它原因促成了這樣的成績提升☂️，不一定就完全是由於訓練所引起運動表現的提升。為了計算SWC，我們計算研究對象間標準差（SD）👨‍🦰，然後將該數字乘以0.2🥲🌛。從圖7和30m的沖刺時間（請看圖中的“ Best_30-m”列）我們可以看到SD為0.16*0.2= 0.032s，這表明對於運動員A而言🚪，30m沖刺時間的SWC將是4.5-0.032=4.468s。

但是👳🏼，回顧一下我們剛剛進行的信度測試也是很重要的，看看我們是否可以準確地檢測到這一個小的變化。在圖6中，我們可以看到30米沖刺時間的CV為2.4％💿。對於運動員A的SCW則是4.5*0.024 =0.108s；因此在此案例中，該運動員和該測試的SWC落在該測試的誤差範圍內，所以該數據不適合使用。在這種情況下，我們可以乘以更大的系數，即0.6或1.2，以便現在分別檢測出屬於中等或較大變化的類別（有關其他系數𓀉，請參見表1）或計算CV。在這方面，使用CV來計算真實的變化並為運動員設定目標數據是個好主意👨‍🦼。然而，在最初的測試中如果有一個錯誤，在接下來的測試中還會有錯誤，雖然已經對前者進行了解釋🙊，但沒有對後者進行解釋。解決方法非常簡單，將CV乘以2即可確定數據的真實變化。如果你的運動員熟悉測試並且被充分地進行管理，則應有可能獲得CV≤3％。

再次以30m沖刺時間與運動員A為例🧑🏿‍💻，註意此CV2.4％的兩倍= 4.8％🧖🏿‍♀️，作為一個體能教練，你設置的第一個真實變化以及目標測試結果應該如下：4.5-（4.5 *0.048 ）=4.5–0.216 =4.284秒🔱。圖8展示了如何使用此方法在Excel中添加一列來計算每個運動員的目標數據。

圖8 公式欄顯示了如何使用雙重變異系數(CV)方法計算第一個有意義的變化🪂。括號中的值從原始數據中減去兩倍的CV，註意，“$”符號固定CV的位置，因此公式可以向下拖動到所有單元格👧🏿。

究竟是使用SWC法還是雙重CV法取決於教練自己。盡管SWC可能會落在測試錯誤的範圍內，但如果CV太高（例如CMJ和RSI，圖5），則雙CV方法可能會設置不切實際的目標。第三種選擇可能是單獨查看每個運動員（或創建子分組）👩‍👩‍👦，因為某些運動員在整個測試中可能足夠一致🧑🏼‍🦰📞，可以使用SWC（為0.2）。另外，如果他們是一名“高水平”的運動員🤷🏻‍♂️，他們只會尋求做出微小而重要的改變👳🏼‍♀️⛲️。

五、效應量

當嘗試量化測試產生表現數據的變化時👳🏿‍♂️，可以使用ES客觀地展示變化的幅度。同樣💮，客觀性在這也是非常關鍵的，因為客觀性消除了關於運動員內部產生的變化質量的任何主觀成分，尤其是當變化可能表示未來的幹預（以及可能的投入）。例如，在口頭描述的情況下，CMJ的測試高度從46cm變到49cm可以認為是中等的變化，或是很大的變化（表1）🤷🏼。當對比隊伍集體水平時，這種變化可以在相同的隊內被量化💂🏼。

ES通常使用公式2中所示的Cohen d計算🧑🏿‍🎨，並且在圖9和10中提供了一個應用示例。但是1️⃣，此處應謹慎使用，教練應意識到以下事實⛰：當運動員是訓練多年的高水平運動員，他們的“微小進步”是與業余運動員“大量進步”是等同的。此外🐧，由於SD是用於計算ES的，因此請確保組內數據是具有同質性的，即具有相同運動水平和運動能力（這樣不會產生過大範圍的測試數據）將有助於發現有意義的變化🏊🏿‍♂️🦨。

因此，作為教練的你可以在這考慮基於訓練年限的不同再分一次亞組，與SWC相似🐧，對於相對更高水平的運動員的數據變化可能會被掩蓋。Rhea（5）測試了3,000個ES涵蓋400項不同的研究🧑‍🦽‍➡️，並提出了一種新的ES分類量表🙏🏽🚪，該量表特定於受試者的力量訓練狀態（表2）🤵🏿。

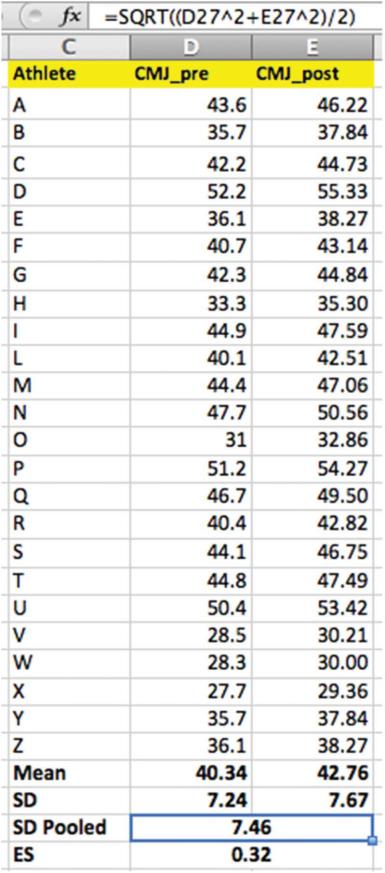
圖9 頂部的公式欄顯示了合並標準差的計算🙌🏽。倍根號5 O;^ 5的𓀚。

六、相關性

相關性描述了可能的關系。它們可以是2個變量之間的正相關、無相關、負相關（或在這種情況2種不同的運動表現測試）🚼。例如💪🏼，力量與垂直縱跳之間具有正相關、力量與速度之間也是正相關、速度與靈敏之間是正相關👱🏻‍♀️。相關性假設了如果我們影響1個變量，那麽這個變量將影響另一個📴。該關系的強度由“ r”值表示，範圍從-1到1，其中0表示無相關性。根據Cohen（1），相關系數閾值0.10為“小”👷🏻‍♂️，0.30為“中”，而0.50為“大”。此外，Hopkins等（4）建議把0.7當做是非常大值（very large），把0.9當做是極大值（extremely large）。

在確定某個關系甚至在統計上具有重要意義之前，需要一定的樣本量🦒。例如🐢🧑‍✈️，在r =0.2的關系被認為是有意義之前，將需要近100位運動員作為樣本量🏄🏽‍♀️；對於r=0.3，則需要大概40名運動員；r =0.5則需要大概14名運動員⛹🏿‍♂️，而r =0.6，則只需要9名運動員（2）👩🏼‍🍳。同樣🐯，如果你的受試者只有6個人🧎🏻‍♂️‍➡️🙎🏽‍♂️，通過上述關系我們可以認為如果r的值小於0.7則這個測試的6人數據將是沒意義的。除非任何數值被認為具有統計意義，否則這些關系被認為是偶然發生的◾️。

我們還可以將r值取平方💅🏼🐕‍🦺，以表示可決系數（coefficient of deternmination ,r2）。這是一個變量的可變性量度，由另一個變量解釋，通常以百分比表示（乘以100%）⚽️。例如🫴🏼，如果力量和速度之間的相關性是r=0.8，則r2=64％（0.8*0.8*100%）😥🍰，即力量變化的64％由速度變化解釋👟。這也告訴我們——剩下的36%可以有其他的變量進行解釋。下面分別在圖12和13中說明了如何使用Excel進行的相關性計算和可決系數✩。

對於各類體育類教練而言，諸如相關性和可決系數之類的統計分析是一種詢證分析工具🐅，因此也是越來越多的在體能訓練領域被使用。例如很多教練無法說明速度對運動競賽中運動表現的重要性。因此🚵🏼‍♀️，若當前一些主流觀念或者是組織管理機構文化🪙、運動員發展受限的情況下👧🏿，但我們可以很好的說明身體素質與力量和跳躍高度具有相關性🤐，那麽這有可能幫助我們更好的推廣、引進抗阻訓練理念。

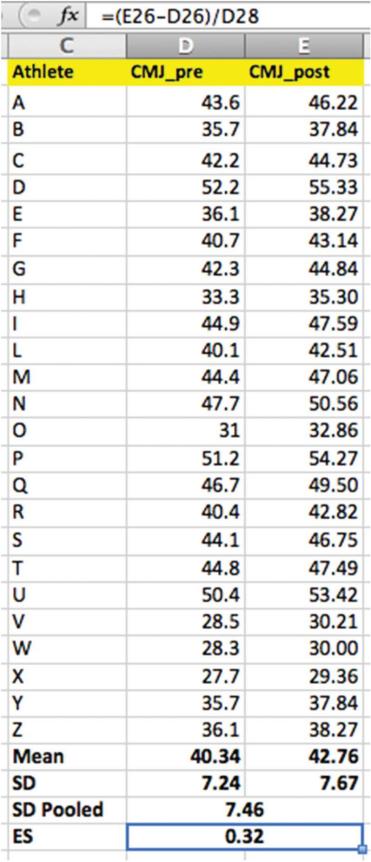
圖10 在計算合並的標準偏差之後🤵🏼‍♀️，編輯欄將顯示效應量的計算。該值（0.32）被視為“小”。

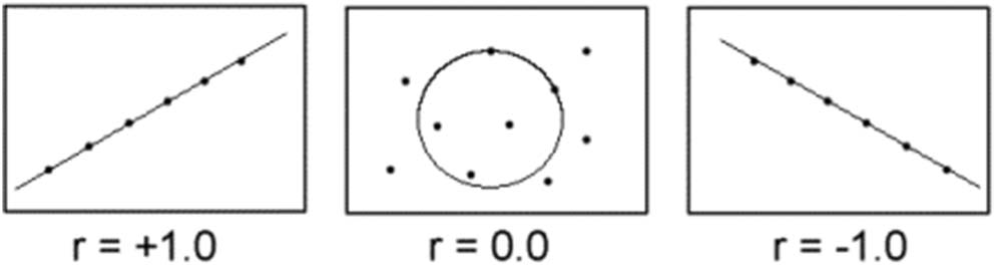
圖11 相關性。從左到右：完全正相關，無相關，完全負相關💌🌰。

圖12 公式欄標識每個相關的計算。打開方括號後，可以高亮顯示感興趣的單元格🥖。

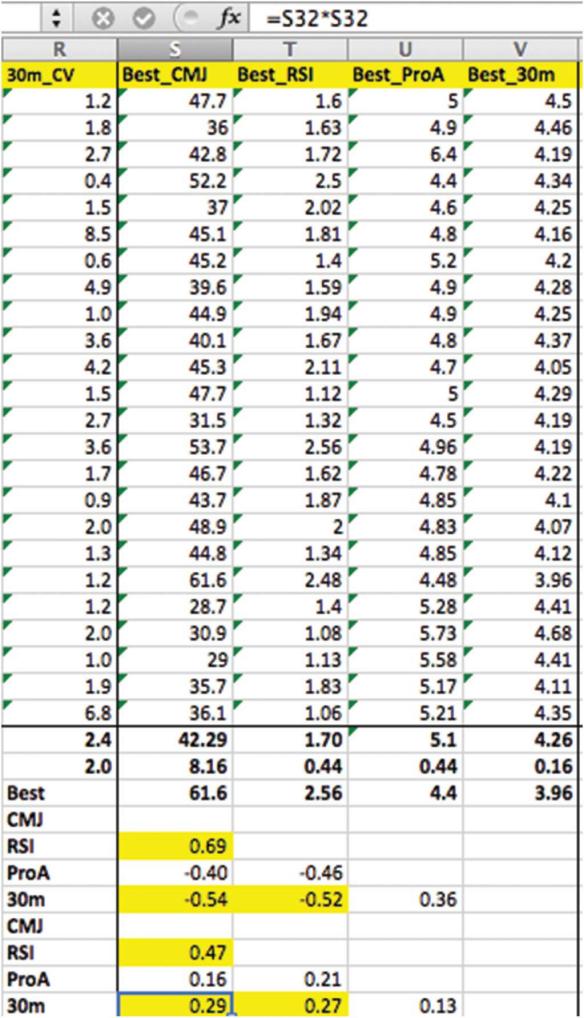
圖13 為了計算可決系數r2，采用相關系數r的平方表示。

七、結論

總言之，數據分析的首要任務是確保所收集數據的質量。這可以通過繪製每個測試的平均數據並評估其系統性偏差來完成💇👅；只要對運動員進行適當的熱身🚀、且測試過程不疲勞並熟悉測試動作，這應該都不是問題。隨後可以使用CV來檢查測試的信度——正如所前文討論的🍠，具有信度的該CV值小於10％🤫🧔🏻‍♂️。但是🐖，進行體能測試時🛍，數據應低於5％🎷。

完成上述步驟後，可以進一步地分析數據以確定訓練的效果。據此，可以使用SWC（或任何其他公式）來設置目標值👩🏽‍🚒，但始終牢記確保這些目標不在CV表示的測試誤差範圍內。如果不是這種情況，則受試者之間的SD可以乘以更大的系數，或者使用的目標是測試CV的兩倍。後者考慮了後續測試的誤差，但如果CV是0.3％時，則可能會產生不切實際的目標。最後一種選擇是使用每位運動員各自的SD或CV設置目標值。

最後，如果將測試數據與同一支球隊或另一支球隊的先前表現進行比較👦🏿🙍‍♀️，則可以使用ES計算數據之間的變化幅度，從而對任何明顯的差異進行客觀評估👨‍👧。此後，為了證明訓練方法和認識到測試中關鍵的身體生理前期需求是如何影響運動表現的🛄，相關性分析必須進行；所有參與測試者應該確保效應量是否闡明了這種關系確實是有意義的一個。

翻譯者：意昂体育42020級研究生  李恒誌

校對者🤚🏽：張鵬

文獻來源：

Turner, Anthony MSc, CSCS*D1; Brazier, Jon MSc, CSCS2; Bishop, Chris MSc1; Chavda, Shyam MSc, CSCS1; Cree, Jon MSc1; Read, Paul MSc, CSCS3 Data Analysis for Strength and Conditioning Coaches, Strength and Conditioning Journal: February 2015 - Volume 37 - Issue 1 - p 76-83

doi: 10.1519/SSC.0000000000000113